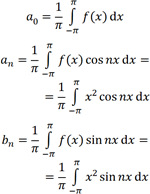Adit Math Engine

Adit Math Engine Screenshots

LaTeX expressions

f(x)= \begin{cases} -x^{2}, &\text{if x < 0;}\\ 
\alpha + x, &\text{if 0 }\leq\text{ x }\leq\text{ 1;}\\ 
x^{2}, &\text{otherwise.} \end{cases}

Align Environment

\begin{align} x &= x \wedge (y \vee z)& &\text{(by distributivity)}\\ &= (x \wedge y) \vee (x \wedge z)& &\text{(by condition (M))} \\ &= y \vee z. \end{align}

Align Environment

\begin{align} h(x) &= \int \left( \frac{ f(x) + g(x) } { 1+ f^{2}(x) } + \frac{ 1+ f(x)g(x) } { \sqrt{1 - \sin x} } \right) \, dx\\ &= \int \frac{ 1 + f(x) } { 1 + g(x) } \, dx - 2 \tan^{-1}(x-2)
\end{align}

Integrals

\int_{\mathcal{D}} | \overline{\partial u} |^{2} \Phi_{0}(z) e^{\alpha |z|^2} \geq c_{4} \alpha \int_{\mathcal{D}} |u|^{2} \Phi_{0} e^{\alpha |z|^{2}} + c_{5} \delta^{-2} \int_{A} |u|^{2} \Phi_{0} e^{\alpha |z|^{2}}

Limit

\lim_{(v, v�) \to (0, 0)} \frac{H(z + v) - H(z + v�) - BH(z)(v - v�)} {\| v - v� \|} = 0

Under and Overset

u \underset{\alpha}{+} v \overset{1}{\thicksim} w \overset{2}{\thicksim} z

Stretch Brackets

\left. F(x) \right|_{a}^{b} = F(b) - F(a)

N-Ary Operators

f(\mathbf{x}) = \bigvee\nolimits_{\!\mathfrak{m}} \left(\, \bigwedge\nolimits_{\mathfrak{m}} (\, x_{j} \mid j \in I_{i} \,) \mid i < \aleph_{\alpha} \,\right)

Summ

\sum_{i = 1}^{ \left[ \frac{n}{2} \right] } \binom{ x_{i, i + 1}^{i^{2}} } { \left[ \frac{i + 3}{3} \right] } \frac{ \sqrt{ \mu(i)^{ \frac{3}{2}} (i^{2} - 1) } } { \sqrt[3]{\rho(i) - 2} + \sqrt[3]{\rho(i) - 1} }

Matrix

\mathbf{A} = \begin{pmatrix} a+b+c& uv\\ a+b&u+v \end{pmatrix} \begin{pmatrix} 30 & 7\\ 3 & 17 \end{pmatrix}

Arrows

A \xleftarrow{\text{this way}} B \xrightarrow[\text{or that way}]{ } C

Big Matrix

\mathbf{A} = \begin{pmatrix} \dfrac{\varphi \cdot X_{n, 1}} {\varphi_{1} \times \varepsilon_{1}} & (x + \varepsilon_{2})^{2} & \cdots & (x + \varepsilon_{n - 1})^{n - 1} & (x + \varepsilon_{n})^{n}\\ \dfrac{\varphi \cdot X_{n, 1}} {\varphi_{2} \times \varepsilon_{1}} & \dfrac{\varphi \cdot X_{n, 2}}  {\varphi_{2} \times \varepsilon_{2}} & \cdots & (x + \varepsilon_{n - 1})^{n - 1} & (x + \varepsilon_{n})^{n}\\ \cdots & \cdots & \cdots & \cdots & \cdots &\\ \dfrac{\varphi \cdot X_{n, 1}} {\varphi_{n} \times \varepsilon_{1}} & \dfrac{\varphi \cdot X_{n, 2}}  {\varphi_{n} \times \varepsilon_{2}} & \cdots & \dfrac{\varphi \cdot X_{n, n - 1}} {\varphi_{n} \times \varepsilon_{n - 1}} & \dfrac{\varphi\cdot X_{n, n}} {\varphi_{n} \times \varepsilon_{n}} \end{pmatrix} + \mathbf{I}_{n}

Gather Environment

\begin{gather*} a_0=\frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x)\,\mathrm{d}x\\[6pt] \begin{split} a_n=\frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x)\cos nx\,\mathrm{d}x=\\  =\frac{1}{\pi}\int\limits_{-\pi}^{\pi}x^2\cos nx\,\mathrm{d}x \end{split}\\[6pt] \begin{split} b_n=\frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x)\sin nx\,\mathrm{d}x=\\ =\frac{1}{\pi}\int\limits_{-\pi}^{\pi}x^2\sin nx\,\mathrm{d}x \end{split}\\[6pt] \end{gather*}